Giải SGK Toán 8 trang 9, 10 Cánh Diều tập 1

Bài 1 trang 9 SGK Toán 8 tập 1 - Cánh Diều

a) Trong các biểu thức sau, biểu thức nào là đơn thức:

(dfrac{1}{5}x{y^2}{z^3};3 - 2{{rm{x}}^3}{y^2}z; - dfrac{3}{2}{x^4}{rm{yx}}{{rm{z}}^2};dfrac{1}{2}{x^2}left( {{y^3} - {z^3}} right))

b) Trong những biểu thức sau, biểu thức nào là đa thức:

(2 - x + y; - 5{{rm{x}}^2}y{z^3} + dfrac{1}{3}x{y^2}z + x + 1;dfrac{{x - y}}{{x{y^2}}};dfrac{1}{x} + 2y - 3{rm{z}})

Phương pháp:

Dựa vào khái niệm đơn thức, đa thức để xác định được các biểu thức đơn thức, đa thức.

Lời giải:

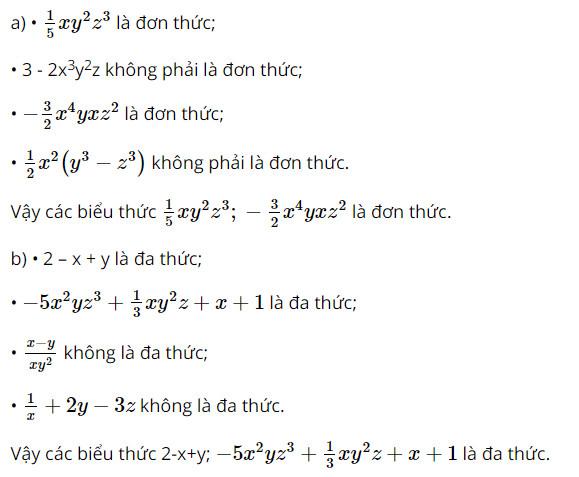
Bài 2 trang 10 SGK Toán 8 tập 1 - Cánh Diều

Thu gọn mỗi đơn thức sau:

a) ( - dfrac{1}{2}{x^2}yx{y^3}) b) (0,5{{rm{x}}^2}{rm{yzx}}{y^3})

Phương pháp:

Ta thu gọn đơn thức bằng cách thực hiện phép nhân lũy thừa cùng cơ số đối với biến.

Lời giải:

Bài 3 trang 10 SGK Toán 8 tập 1 - Cánh Diều

Chỉ ra các đơn thức đồng dạng trong mỗi trường hợp sau:

a) ({x^3}{y^5}; - dfrac{1}{6}{x^3}{y^5}) và (sqrt 3 {x^3}{y^5}) b) ({x^2}{y^3}) và ({x^2}{y^7})

Phương pháp:

Các đơn thức có phần hệ số khác 0 và có cùng phần biến là những đơn thức đồng dạng.

Lời giải:

Bài 4 trang 10 SGK Toán 8 tập 1 - Cánh Diều

Thực hiện phép tính:

a) (9{{rm{x}}^3}{y^6} + 4{{rm{x}}^3}{y^6} + 7{{rm{x}}^3}{y^6})

b) (9{{rm{x}}^5}{y^6} - 14{{rm{x}}^5}{y^6} + 5{{rm{x}}^5}{y^6})

Phương pháp:

Để cộng (trừ) các đơn thức đồng dạng ta cộng (trừ) các hệ số với nhau và giữ nguyên phần biến.

Lời giải:

a) 9x3y6 + 4x3y6 + 7x3y6 = (9 + 4 + 7)x3y6 = 20x3y6;

b) 9x5y6 - 14x5y6 + 5x5y6 = (9 - 14 + 5)x5y6 = 0.

Bài 5 trang 10 SGK Toán 8 tập 1 - Cánh Diều

Thu gọn mỗi đa thức sau:

a) (A = 13{{rm{x}}^2}y + 4 + 8{rm{x}}y - 6{{rm{x}}^2}y - 9)

b) (B = 4,4{{rm{x}}^2}y - 40,6{rm{x}}{y^2} + 3,6{rm{x}}{y^2} - 1,4{{rm{x}}^2}y - 26)

Phương pháp:

Ta nhóm các đơn thức đồng dạng với nhau và thực hiện phép tính.

Lời giải:

Thu gọn mỗi đa thức, ta được:

a) A = 13x2y + 4 + 8xy - 6x2y - 9

= (13x2y - 6x2y) + 8xy + (4 - 9)

= 7x2y + 8xy - 5

b) B = 4,4x2y - 40,6xy2 + 3,6xy2 - 1,4x2y - 26

= (4,4x2y - 1,4x2y) - (40,6xy2 - 3,6xy2) - 26

= 3x2y - 37xy2 - 26.

Bài 6 trang 10 SGK Toán 8 tập 1 - Cánh Diều

Tính giá trị của mỗi đa thức sau:

a) (P = {x^3}y - 14{y^3} - 6{rm{x}}{y^2} + y + 2) tại x =-1; y = 0,5

b) (Q = 15{{rm{x}}^2}y - 5{rm{x}}{y^2} + 7{rm{x}}y - 21) tại x = 0,2; y = -1,2

Phương pháp:

Thay các giá trị x, y cho trước vào các đa thức rồi thực hiện phép tính.

Lời giải:

a) Thay x = -1 , y=0,5 vào đa thức P ta được:

(begin{array}{l}P = {left( { - 1} right)^3}.0,5 - 14.0,{5^3} - 6.left( { - 1} right).0,5^2 + 0,5 + 2P = - 0,5 - 1,75 + 1,5 + 2,5 = 1,75end{array})

Vậy đa thức P = 1,75 tại x = -1; y = 0,5

b) Thay x = 0,2; y = -1,2 vào đa thức Q ta được:

(begin{array}{l}Q = 15.0,{2^2}.left( { - 1,2} right) - 5.0,2.{left( { - 1,2} right)^2} + 7.0,2.(-1,2) - 21Q = - 0,72 - 1,44 - 1,68 - 21 = -24,84end{array})

Vậy Q = -24,84 tại x = 0,2; y = -1,2

Sachbaitap.com