Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh

Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh

Đề bài: Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?

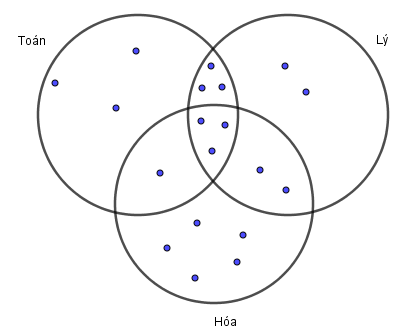
Theo giả thiết đề bài cho, ta có biểu đồ Ven:

Dựa vào biểu đồ Ven ta thấy:

Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là:

6 - 3 = 3 (em)

Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là:

4 - 3 = 1 (em)

Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là:

5 - 3 = 2 (em)

Số học sinh chỉ giỏi một môn Toán là:

10 - 3 - 3 - 1 = 3 (em)

Số học sinh chỉ giỏi một môn Lý là:

10 - 3 - 3 - 2 = 2 (em)

Số học sinh chỉ giỏi một môn Hóa là:

11 - 1 - 3 - 2 = 5 (em)

Số học sinh giỏi ít nhất một trong ba môn là:

3 + 2 + 5 + 1 + 2 + 3 + 3 =19 (em)

Đáp số: 19 em

* Phương pháp giải toán sử dụng biểu đồ Ven:

+ Bước 1: Chuyển bài toán về ngôn ngữ tập hợp.

+ Bước 2: Sử dụng sơ đồ Ven để minh họa các tập hợp.

Vẽ các vòng kín đại diện các tập hợp (mỗi vòng kín là một tập hợp), lưu ý hai vòng kín có phần chung nếu mỗi vòng kín có ít nhất một phần nằm trong vòng kín kia và hai tập hợp đó khác rỗng.

+ Bước 3: Dựa vào sơ đồ Ven ta thiết lập được đẳng thức hoặc phương trình, hệ phương trình, từ đó tìm được kết quả bài toán.

Lưu ý:

+ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) - n(A ∩ B).

⇒ n(A ∩ B) = n(A) + n(B) - n(A ∪ B).

+ Nếu A và B không có phần tử chung, tức là A ∩ B = ∅, thì n(A ∪ B) = n(A) + n(B).

Xem thêm các bài viết liên quan hay chi tiết:

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác: